（譯者註：本文所介紹的技術在密碼學社區裡一般稱為“KZG10 承諾”，得名於論文三位作者的姓氏首字母。但在介紹到以太坊生態中時，被簡化成了“ Kate 承諾”，甚至連核心開發者也是這麼稱呼的。這是對另外兩位作者的不尊重，不應該繼續下去。在本譯文中，凡原作者使用“Kate commitment” 的地方，都一律譯為“KZG10 承諾”。）

免責聲明 ：本文僅僅是匯集、鏈接了許多已經公開的成果，對應的榮譽（包括本文所鏈接的圖片）應歸屬於相應的作者/開發者。

PS ：特別感謝Ethereum R & D discord 頻道（尤為感謝 @vbuterin 和@piper）幫助我理解KZG10 承諾的某些方面。此外，還要感謝 @vbuterin 幫忙審校本文。

PPS ：本文是出於lodestar 團隊的利益而撰寫的；lodestar 是一個很棒的ETH PoS 客戶端，基於typescript，可以讓以太坊的服務無處不在，也開啟了作者對以太坊生態和創新的理解。

我希望本文也能對全世界的其他開發者/技術人員有所幫助。本文遵循CC0 自由創作公約，作者已放棄所有權利。

動機

作為一個有益的指南，幫助讀者熟悉、總結以太坊背景下 KZG10 承諾的提議用法，並提供深入理解的指南。

本文的目的更多是總結，而非嚴謹，不過，您可以點擊文中所附的鏈接，它們會有更詳細的解釋。

基礎原理

注-1：哈希值就是一個對被哈希的原像的承諾，用於檢驗被哈希的數據的完整性。 （譯者註：這話其實不是很嚴謹。因為哈希函數往往難以滿足“承諾方案” 所需的性質。）

舉個例子，假設h1 = H(t1, t2, t3..)，然後把h1 交給驗證者（比如，把它放在區塊頭內），然後給出一個偽造的區塊(t1,t2' ,t3...)，對方快速計算這個偽造區塊的哈希值之後，發現兩者對不上，就可以合理地拒絕你的偽造區塊。

類似的，一棵默克爾樹的根節點，就是對按特定索引（路徑）組織起來的所有葉子節點的承諾。或者簡單來說，是對 indexes => values（從索引值到數值）的映射的承諾。

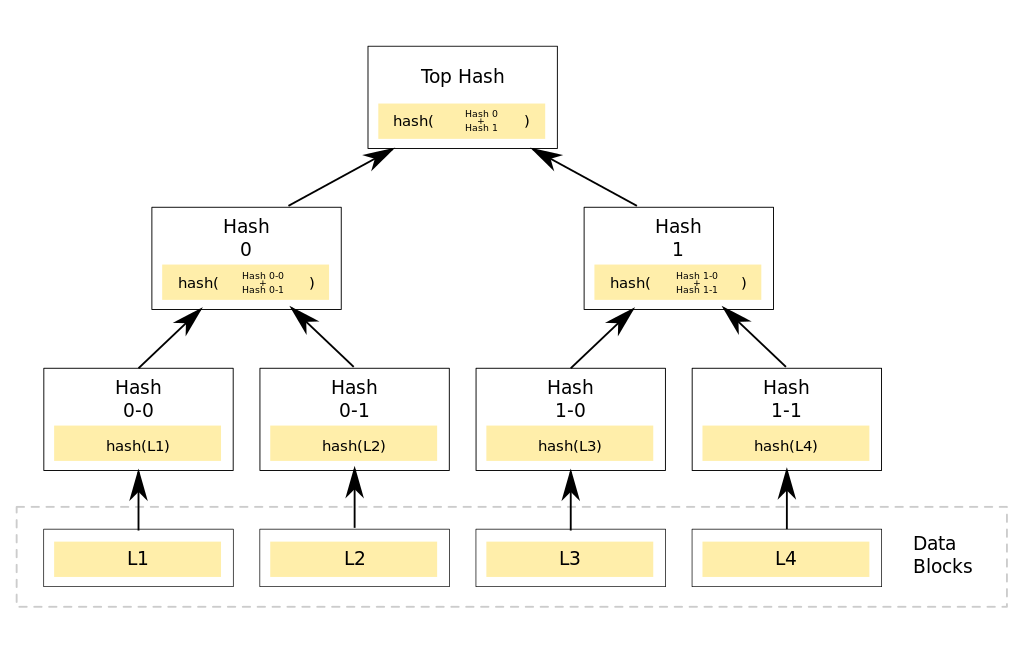
而這裡的“證明” 就是一個葉子的默克爾分支（merkle branch） 以及（這個分支在每一層上的） 兄弟哈希值（sibling hashes），憑藉這些數據，可以逐級向上哈希，並通過最終的哈希值是否與根節點一致來判斷該葉子是否與這棵默克爾樹一致（存在於這棵默克爾樹上）。

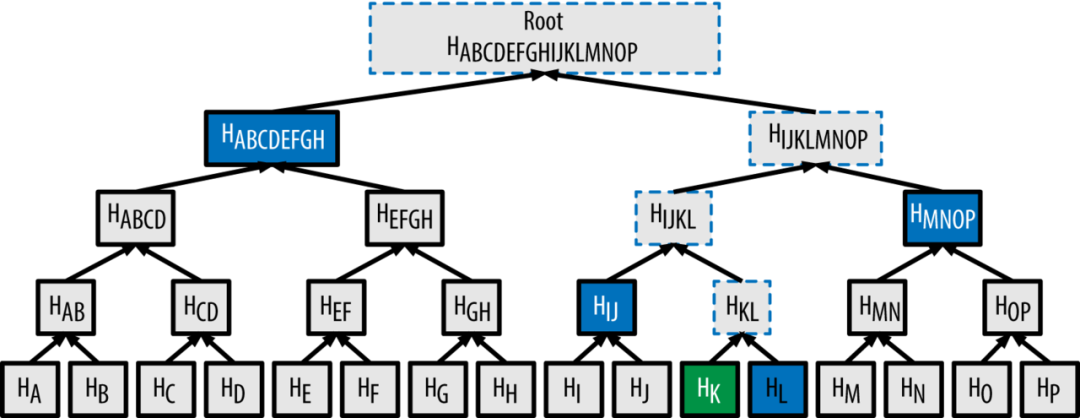
可看看這裡的介紹 : )。

注-2：數據映射與一個多項式的對應關係

indexes => values 這樣的數據映射可以表示為一個多項式 f(x)，並且 f(index)=value（由拉格朗日插值法可知滿足這個條件的多項式必定存在）。 “ f(index)=value ”通常被稱為 求值形式，而“ f(x)=a0+ a1.x + a2.x^2... ” 則是其 係數形式。直觀來說，我們其實是根據映射中所有的 (index,value) 點，擬合出了一個多項式。

為了簡便計算，並確保多項式與數據映射的一一匹配，我們不使用索引值來作為f(x) 的x，用的是w^index，也就是f(w^index)=value，其中w 是d 次單位根（即w^d = 1 且w 是一個複數），而d 是該多項式的次數（也是我們能夠包含的索引值的個數上限）。因此，我們可以使用快速傅立葉變換來實現高效的多項式計算，比如乘法和除法，在求值形式下其計算複雜度會是O(d)，而且可以在O(d*log(d)) 的複雜度內轉化回係數形式。所以保持 d 數值較小還是很有好處的。

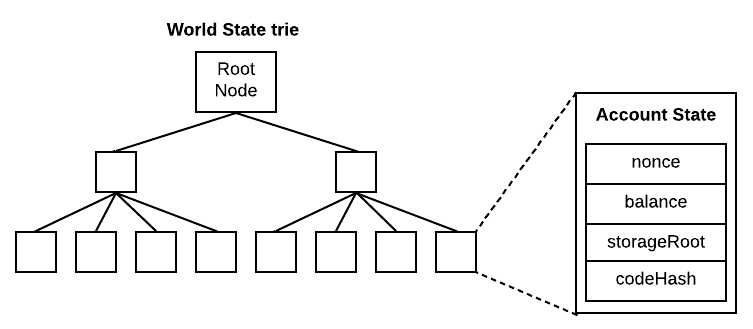
注-2.1：以太坊的狀態是一個從地址到賬戶狀態（addresses => (version,balance,nonce,codeHash,storageRoot)）的映射。

背景知識

以太坊當前使用默克爾樹（更具體一些是“帕特里夏默克爾樹”）作為EVM 數據（EVM 狀態、區塊事務及事務收據，也許還有最近的合約代碼）的承諾。此種承諾方式可以：

逐個區塊地插入/更新數據，以增量的方式產生新的根哈希（即承諾）驗證者可以逐個區塊（甚至逐筆事務）地校驗和證明

前綴樹結構在這裡提供了這種逐塊更新的特性。

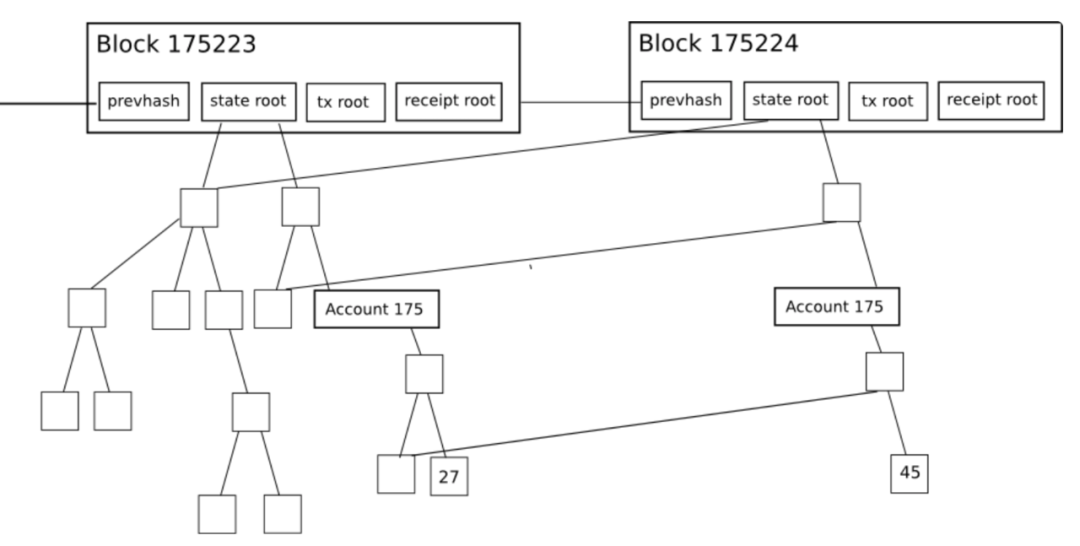
給定一個d 叉的、有N 個葉子的前綴樹，任意更改一個葉子節點，都需要更新O(log-d(N)) 個節點（也就是該葉子與根節點相連路徑上的節點數量）以計算反映新狀態的新根值；而這需要額外的(d-1)*O(log-d(N)) 個兄弟節點哈希值/承諾來用作時間和空間（假設要服務於輕節點）的見證數據（witness）。一個區塊可視為一個需要更改m 個隨機葉子的批量更新，且m<。因為預計只有一小部分的節點可以共享witness 和計算，所以，每次更新的Order（複雜度）不會有太大改變。

在下列情況下，問題還會變得更加嚴重（因為見證數據的規模）：

部分採用快速同步的協議，比如beam sync（光子同步），會下載并快速驗證區塊頭來追上最新的主鏈頂端並參與網絡的共識，注意，它不會先行構建好完整的狀態再參與共識，而是（在共識中）通過獲取錯過的/未加載的狀態的見證數據，來逐步構建出完整的狀態為輕節點服務的時候，他們只關心自己，只想獲得區塊鏈狀態的特定部分網絡走向完全無狀態時，所有的事務和合約操作，都要附帶相關的見證數據，來證明數據輸入和輸出的正確性（譯者註：粗體為譯者所加）在驗證者會被混洗到不同分片的區塊鏈分片模型中，要讓驗證者每到一個分片就構建完整狀態是不現實的代碼默克爾化，訪問代碼時需要附帶這些代碼塊的見證數據在狀態保質期協議中，訪問過期的賬戶需要重新附帶狀態見證數據，以便重建該賬戶的狀態

（譯者註：需要解釋的是，在當前的以太坊網絡中，事務和區塊不會附帶上文所述的見證數據。即，網絡所傳播的見證數據規模與事務/區塊的規模無恆定的關係。前兩種情形恰好是在當前以太坊協議下為數不多的、需要傳播見證數據的情形。我們關心狀態數據的規模，完全是出於一種協議改進方向—— “無狀態性” 的需要。後面四種情形都跟無狀態性有關，當然都比理論上要傳播的數量更多。但是，以上述的理論計算來作為基準點去比較，本身是不合適的—— 連代碼默克爾化這種在無狀態下節省狀態數據的方案，也會被歸為讓情況更嚴重的方案。）

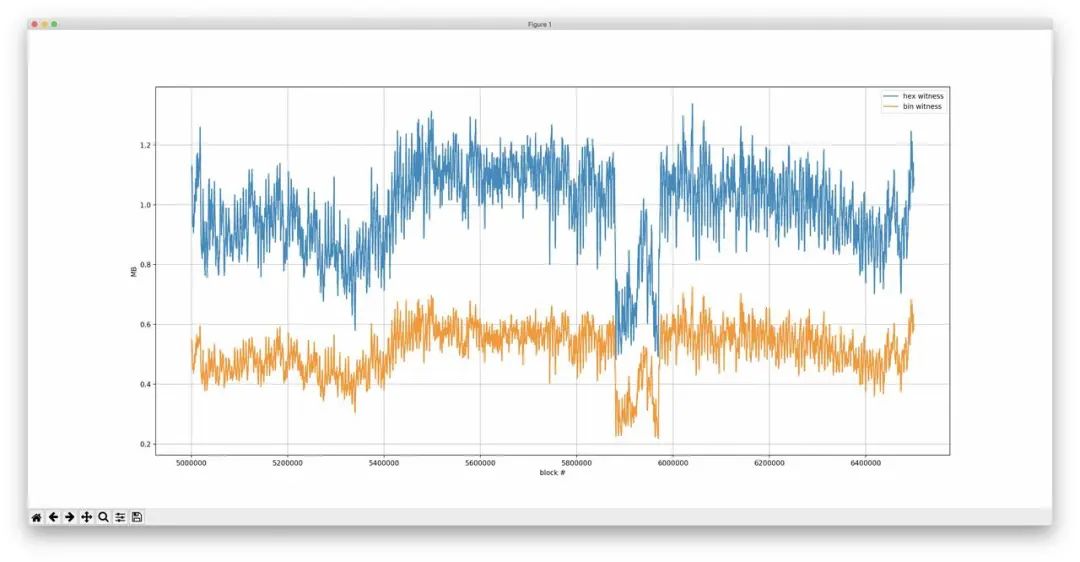
在無狀態以太坊項目的一個實驗中，出現了 1 MB 的區塊證據（其中大部分都是默克爾證據），在發生攻擊的時候還會膨脹好幾倍。

其中一種解決辦法是轉為使用“二進制默克爾樹”，也就是把d 降下來，這樣雖然樹的深度（高度）會增加，但仍然是O(log(N)) 的規模。

為什麼要使用KZG10 承諾？

對於要放在區塊頭內承諾數據的承諾方案來說，以下特點是理想屬性：

證據的數據量較小，可以塞進區塊頭里，且仍具有很強的安全保證易於證明某個承諾是使用分組化數據（chunkified data）的一個子集生成出來的足夠小，最好證據的數據量是恆定的為了跟踪數據，承諾應當易於以增量的形式變更

基於KZG10 承諾的方案就是大家一番搜尋的結果。

- 譯者註：可以看到，作者有三個-

什麼是KZG10 承諾？

KZG10 承諾可以視為另一種哈希方案，只不過它哈希的不是“字節”（數據），而是多項式。

實際上，它就是計算（evaluation） 多項式f(x) 在秘密的定點s 上的值，只不過它們都是表示在一條橢圓曲線上的，也即[f(s)]=f([s] )。這需要一個受信任的啟動設置（跟zcash 區塊鏈的創世活動一樣），來生成[s]、[s^2]、… [s^d]（以便在多項式需要x^i的地方插入），而d 就是多項式的最大階數。

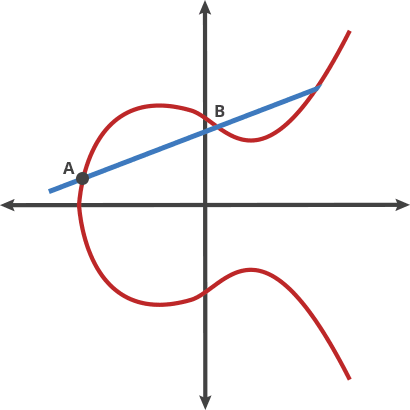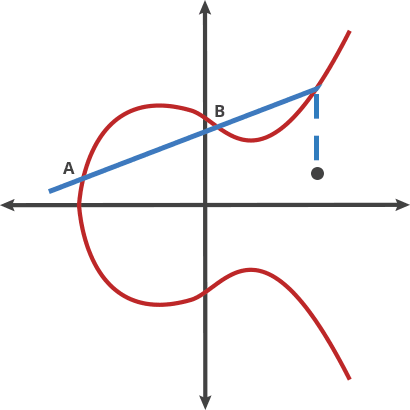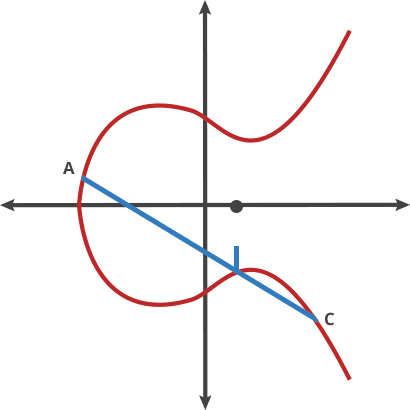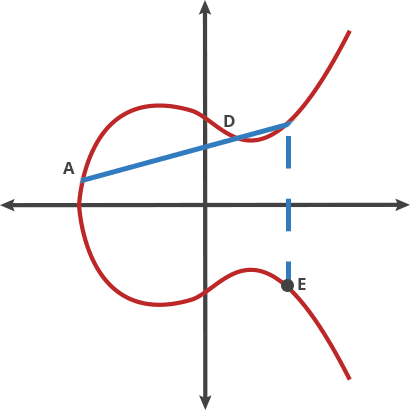
這裡的[t] 表示點t 處的橢圓曲線值，也就是t[1]，是橢圓曲線加法群的生成點（[1]）相加t 次（等同於對Fp 求模，modulo Fp ）。橢圓曲線上的所有計算都是對Fp 求模，Fp 給曲線施加了一定的範圍（譯者註：Fp 是一個由p 個元素組成的有限域，限制了該橢圓曲線值的範圍）。

注3.0：在 indexes=>values 的映射中，所有的值都要表示為一條橢圓曲線上的元素，即[value]，以便計算承諾（後文有詳述）。這就使得value 的大小有了限制（為了要成為 modulo Fp 的值）。在BLS 曲線上，大概在31～32 字節之間。為了簡便，value 的大小就限制在31 字節，任意更大的值都要分塊化，並用其索引值來恰當地表示（或者截斷）。

注3.1：[t] 可以被視為t 的哈希值，因為從[t] 找回t 是個離散對數問題（discrete log problem），對於安全的曲線來說，是很難做到的。

注3.2：s 是一個秘密的數值，永遠不應洩漏給任何人/所有人，但橢圓曲線點[s], [s^2]…[s^d] 及其在另一條橢圓曲線上的值[s]' （其生成點為[1]' 且只需知道[s]' ）則應生成並公開出來，讓所有人知道。這就是啟動設置要做的事。

這些 系統參數 定義了整個系統的安全性，因為s 暴露會使得攻擊者可以構建任意內容的 證據。因此，一個有N 個參與者共同參與的啟動設置儀式中，他們要通過協議把本地的s 結合起來，這樣只要有1 個參與者是誠實的、在參與之後就銷毀掉了自己提供的s，這個系統就會是安全的。即，信任模型是1/N 模型，N 越高，風險就越低。

注3-3：[] 是一個線性的操作，即[x]+[y]=[x+y]，而且 a[x]=[ax]。如果上所述，我們將數據映射（索引值=> 數值）表示為f(w^index)=value，即一個多項式的求值形式，也可說，我們用這些(w^index,value) 點擬合出了一條曲線（多項式）。

所以，一個多項式f(x) 的KZG10 承諾c(f) 是一個橢圓曲線點f([s])，這個點可以靠在f(x) 的展開式中插入[s],[s^2] … 計算得出。

注3-4：f(s) 是無法計算的，因為s 是個秘密值。但是 C(f)=[f(s)]=f([s]) 是可以計算的。

注3-5：f(x)的承諾 C(f)=[f(s)] 也是一個線性的運算符，即，C(f+g)=C(f)+C(g)。

Rollup/聚合器 可以使用這一屬性來更新承諾。在求值形式下，更新一個求值點將導致f(x) 完全改變，但因為有這個屬性，其承諾c(f) 仍然是易於更新的。

（未完）

（文內有許多超鏈接，可點擊左下”閱讀原文“ 從EthFans 網站上獲取）

原文鏈接:https://hackmd.io/yqfI6OPlRZizv9yPaD-8IQ

作者: g11tech

翻譯: 阿劍