作者:比原鏈王嘉昊、劉秋杉
前言——《AMM終極筆記》是對諸多代表性AMM 項目和相關論文進行的一項綜述(survey),由於AMM 所涉及層面較為廣泛,本文選取我們認為最能代表AMM 本質特徵以及未來發展方向的無常損失進行講解。
注:AMM(Automated Market Maker),自動化做市商,以基本數學曲線定義加密貨幣交易對的供需曲線,基於智能合約的全天候無人值守,重新定義了DEX 的基本形態,代表項目Uniswap。
大家最為關心的無常損失是一個難題,不可解,但存在優化的方法。
從簡單的角度來說,無常損失就是當場外(AMM 資金池外的主流交易市場)代幣A 相對於代幣B 的匯率上漲時,套利交易者會從場外籌集代幣B,並轉移到AMM 資金池,以相對於場外更優惠的匯率換得更多的代幣A,從而實現無風險套利。而這部分利潤也是資金池(LP)的損失,可以稱之為無常損失(臨時損失),因為一旦匯率又重新回到原始位置,將再次創造反向套利空間(對稱的),整體池子的資產數量將回歸到原始狀態,LP 們無損失,但因為行情的兩次變化,也因此造福了兩次套利者利潤,這個利潤空間就不再來自於LP 的財富,而是市場機會,是只有精明的套利者不斷盯市場贏得的機會。從這個角度看,無常損失是精明的套利者和怀揣大局意識的LP 之間博弈均衡的結果,套利者也極大地活躍了AMM 交易市場,尤其是當有非常多的套利者開始意識到此處的機會並開始競爭套利。
從一般性的角度定義無常損失,即無常損失只看交易對匯率是否發生變化,一旦發生變動,便產生客觀的無常損失,與是漲是跌無關,一旦匯率回歸,損失自動消失。這意味著,只有當流動性提供者(LP)在與最初使用的價格情況不同的情況下移除流動性時,才會出現無常損失。如果不移除,而等待一個更有機會的時機撤出,損失就不會發生。作為對比,在傳統金融上,我們可以認為這是一個 '賣出永續跨期 '的頭寸。之所以說是永續,是因為這個頭寸沒有到期日,LP 可以持有多久就持有多久。
另外要著重提到的一點,也是如今很多玩家都未意識到的一個方面,無常損失雖然理論上是無上限的,但基於比特幣等大行情的變動總是有所範圍的假設,無常損失也是有可計算的上限,例如交易對BTC/USDT 中BTC 從20000 USDT 漲到60000 USDT,留給套利者的無常損失空間也不會超過13%,即LP 無常損失控制在13%(無常損失計算器:https://yieldfarmingtools.com/tools)。
此外,無常損失是一種貪婪心理,我們總是愛將現實和假如做對比,還是看BTC/USDT 交易對,在BTC 上漲後,本質上不論怎麼無常損失,LP 的財富總是法幣增值的,然而人們往往愛跟假如做對比,會想“假如自己當初在20000 USDT 的時候一直持有這麼多BTC 而不去參與AMM 賣掉該多好”,但實際上很多LP 是因為AMM 才開始組建自己的資產配置,去購買BTC,去構建交易對,因此大多數LP 財富增值的機會正是來自於AMM 這種集儲蓄利息與基金組合功能於一身的特定場景,如果總是抱著貪婪的心態去看待問題,那麼可以肯定任何金融市場均不存在只有收益沒有風險的路徑。
附: 以下為模擬交易:(1)當1 ETH = 500 USDT,做市商存入10 ETH 和5000 USDT。他的總資產價值是10000 USDT。 (2)當1 ETH = 550 USDT,這個時候就存在套利的空間,在AMM 機制下,做市商池就會自動向套利者賣出ETH 換取USDT,因此,目前流動性池中資產變為9.53個ETH 和5244 個USDT,對應的ETH 的價格為550 USDT,總資產價值是10488 USDT。 (3)如果不去做市,USDT 本位的價值為10500,這便產生了相對的12 USDT 無常損失。相反的,(a)當價格下跌1 ETH = 450 USDT 時,套利者會向池子注入ETH 來換取有利潤空間的USDT,直到ETH 的場內價格與市場價相同,因此做市商的流動池就變為10.54 ETH 和4743 USDT,總資產價值是9486 USDT。 (b)如果不進行做市活動,總資產價值是9500 USDT。相對來看整體資產貶值了500 USDT,進行做市額外還損失14 USDT。從實際例子中不難看出不論價格漲跌,在AMM機制下,流動性供應商的反向操作都會造成一定的無常損失。
1 動態權重的恆定加權幾何平均函數
此類解決方案以Bancor V2 為代表項目。最原始的靈感是Balancer 為AMM 引入了恆定幾何加權平均的函數:
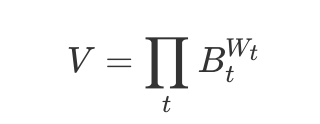
本質跟Uniswap 的恆定乘積類似,但賦予了每一項指數(權重)的概念,也因此擁有更靈活的曲線形態。也是Balancer 第一次在一篇文章(Interest-Bearing Stablecoin Pools Without Impermanent Loss https://medium.com/balancer-protocol/zero-impermanent-loss-stablecoin-pool-with-lending-interests-a3da6d8bb782)中提到了可以通過動態更新權重項來從根源上阻止無常損失的發生,而Bancor V2 則對此方案進行了更通用細緻的數學描述(Calculating Dynamic Reserve Weights in Bancor V2 https://blog.bancor.network/ calculating-dynamic-reserve-weights-in-bancorv2-538b901bcac4)(pdf 版本https://drive.google.com/file/d/1lYsaUi5du7BdP5eXgVJX60POcg2UkBfZ/view)。
細緻的數學描述這裡不展開講解,由於篇幅限製本文只進行原理概要。如果權重項不變的話,可以將曲線形態看成跟Uniswap 一樣。如果不斷變化權重,曲線將會繞著曲線上的某一個點在不斷旋轉,使得旋轉後的曲線在該點的切線斜率(即匯率)與最新的市場價格保持一致,而促進這個旋轉計算的便是來自外部市場價的預言機驅動,通過為AMM 更新每一刻最新的市場價,反推權重項的計算,以使當前點(池子兩資產數量組成的點)在新曲線的切線斜率不斷隨市場變化,進而不創造套利空間。形象的計算如下:
雖然此類解決問題的方法是非常本質的,但缺陷也是十分明顯且隱患巨大。一個本來可以完全自動應對市場的AMM 需要單點依賴一個外部預言機,一旦預言機出現問題,即便是很小的問題,也會給AMM 帶來巨大的套利攻擊損失,這種損失不同於無常損失,是切切實實的用戶損失,也會給以後AMM 的商業擴大帶來根本阻力。另外,此類AMM 將徹底失去市場定價權,即放棄了自己成為Primary Market,我們都知道隨著DeFi 等的崛起,越來越多有價值的新資產都選擇DEX 作為自己的Primary Market,反而那些中心化的主流交易所成了Secondary Market。
除了Bancor V2,國產項目DODO 也有著類似的方式,雖然DODO 並未採用恆定加權幾何平均函數,而是採用了一種類似Curve 的混合構造函數,但本質都是依賴一個外部預言機,來不斷更改【定價/交易】曲線的形態,使得新曲線的報價結果與外部市場緊密跟隨。
如果一個系統只依賴自己,那麼它的安全邊界就是自己,是可以計算的;如果一個系統依賴了外部因子,它的安全邊界理論上是不可估算的,如同一個拜占庭分佈式系統一樣,沒有任何經驗觀察甚至形式化數學可以估算覆蓋到所有潛在fault(故障)路徑。
2 虛擬餘額限制套路路徑
此類僅存在於Mooniswap。與Bancor V2 和DODO 解決問題的思維不同,Mooniswap 並未改變AMM 的最大本質(自動自主定價),與Uniswap 只能眼睜睜看著套利者來吃肉不同,當系統出現套利空間時,Mooniswap 會自動根據偏移量逐次構建多條虛擬的曲線,使得套利交易者只能吸收到每一條虛擬曲線所規定的套利上限,而不再是一次性在原始曲線上完成大量套利。
如下圖,初始平衡點在A,一筆交易使得系統處於X 點,此時便產生了套利空間,在Uniswap 這種傳統AMM 中,任何聰明的套利者都可以通過一筆交易一次性地拉回到A 點,而這個過程往往伴隨著可觀的利潤。 Mooniswap 的虛擬構造法便是陸續構建了上面三條AMM 曲線,首先給套利者呈現的是下圖第二條曲線BC,套利者的套利路徑僅僅只有B 到C 的短暫過程,當該套利者到達C點後,系統便放出第二條虛擬曲線DE,同理,給套利者呈現D 到E 的套利路徑,在第二個套利者到達E 點後,系統放出最後一條曲線,也是最終要更迭到的實際曲線ZQ,最後一位套利者從Z 到Q 完成套利,最終系統曲線變為ZQ,且平衡點為Q。通過者一系列虛擬構造,即便三次加起來的套利空間也遠小於傳統AMM 曲線一次套利路徑,而且在這個過程中套利者也為資金池注入了更多的資產,使得池子規模變大,也充當了LP,曲線向右上偏移。
對於具體的點位計算和數學證明,請詳見Mooniswap 白皮書(Mooniswap https://mooniswap.exchange/docs/MooniswapWhitePaper-v1.0.pdf)。
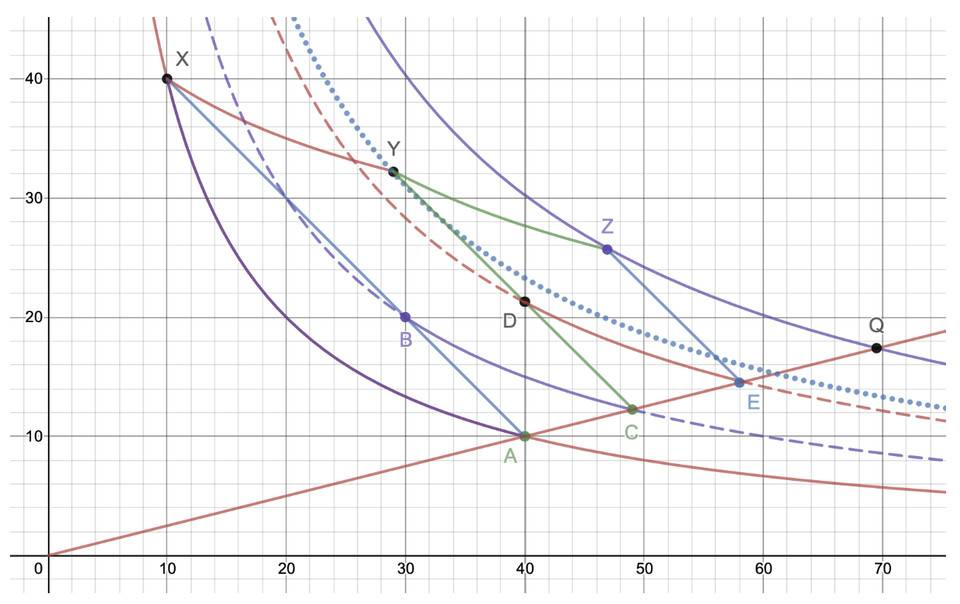
此類方法缺點,需要仔細判別套利機會的出現,一定程度上也需要依賴外部因子;而且虛擬量縮短套利路徑的過程需要動態構建大量曲線,對於高並發的系統,此類方法在工程上過於復雜,引入太多不確定性。
3 無限網格策略做市
以比原鏈MOV 超導V2 提出的基於無限網格策略的AMM 算法為例(暫未實現)。這種解決方案並未直接去關注無常損失的發生(如前第一類),也未去針對無常損失的始作俑者套利者(第二類),它是在以一種基金經理的角色在管理LP的財富,不希望只通過儲蓄利息(手續費)讓LP 財富增值,更是希望可以在專業基金策略的作用下充分利用好LP 巨大的財富池,跟隨市場大勢,獲得基金式的財富增值。其中,無限網格策略是MOV 超導V2 所選擇的方向,並將其在AMM 上實現,雖然還有很多不足,但如下大致給出了構建思路。
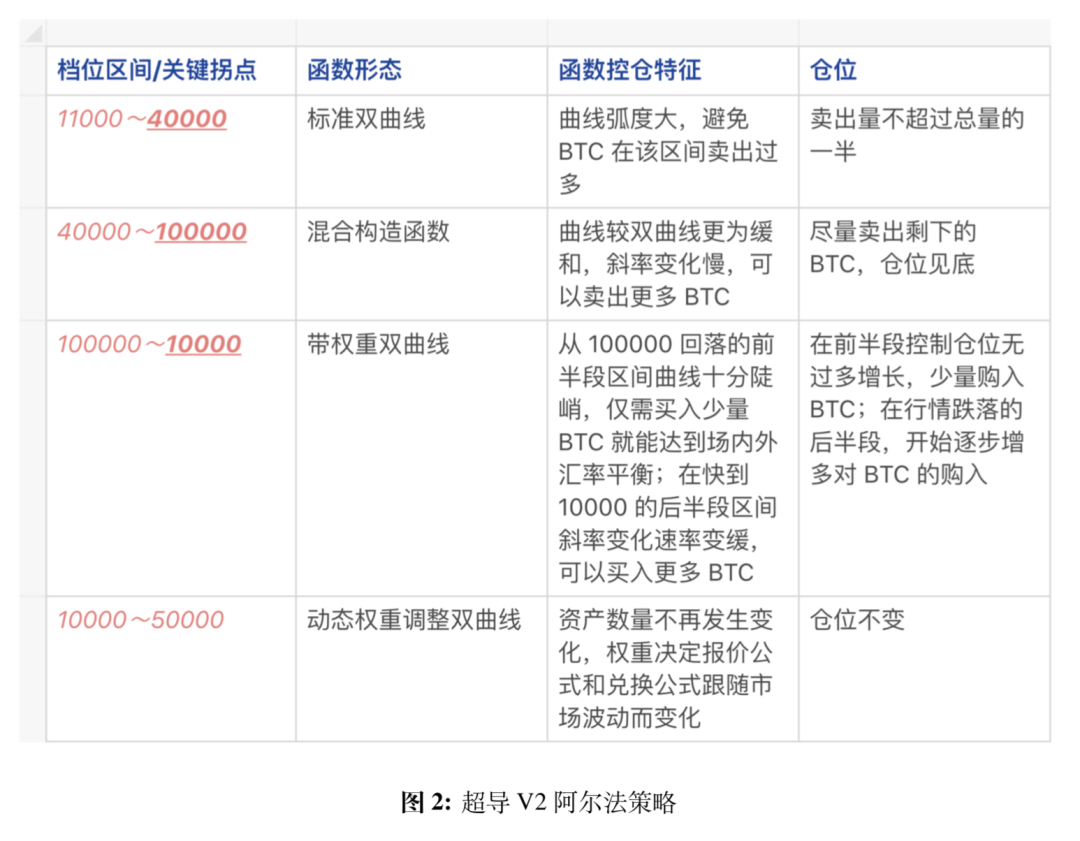
如上圖,超導V2 在原有恆定乘積曲線做市商機制的基礎上進一步分段構造出了不同形態的曲線形態,以滿足無限網格的基本定義——“分段買入賣出,即便在市場最高點時也有現貨可以賣出,在市場最低點時也能完成建倉操作”。超導V2 通過上面四種分段函數的構造,希望可以實現——“在行情上漲時,能夠適當出貨BTC,但不要大量出貨,逐步逐量,既能夠幫LP 在達到最高點前守住BTC,也能夠在上漲行情中智能化的賣出適當數量BTC,以應對潛在的大跌風險;在行情下跌時,HOLD,以上漲時積累的USDT 財富獲得財富增值”。
在具體函數構造和實現原理上,可以對照上圖看如下圖例。早在2020 年8 月份(BTC 11000 刀,超導V2 理論剛剛誕生時),當時的超導V2 設計者就預計未來可能會達到一個40000 刀至100000 刀的一個牛市行情,因此做瞭如上四個分段預測。在第一段中,超導函數為非常普通的恆定乘積曲線,執行簡單的AMM 倉位策略,在達到40000 刀時,函數自動觸發切換為混合構造函數曲線,這是一種曲率更低的曲線,可以大幅度改變BTC 倉位,在40000 ~ 100000 範圍,如果判斷本輪最高點可能到100000 刀,則在100000 刀處再次設置函數切換點,變為非常陡峭的雙曲線,可以幫助LP 在行情回落過程中不會重新將高點套現的USDT 再還回去。具體數據可以見下圖。
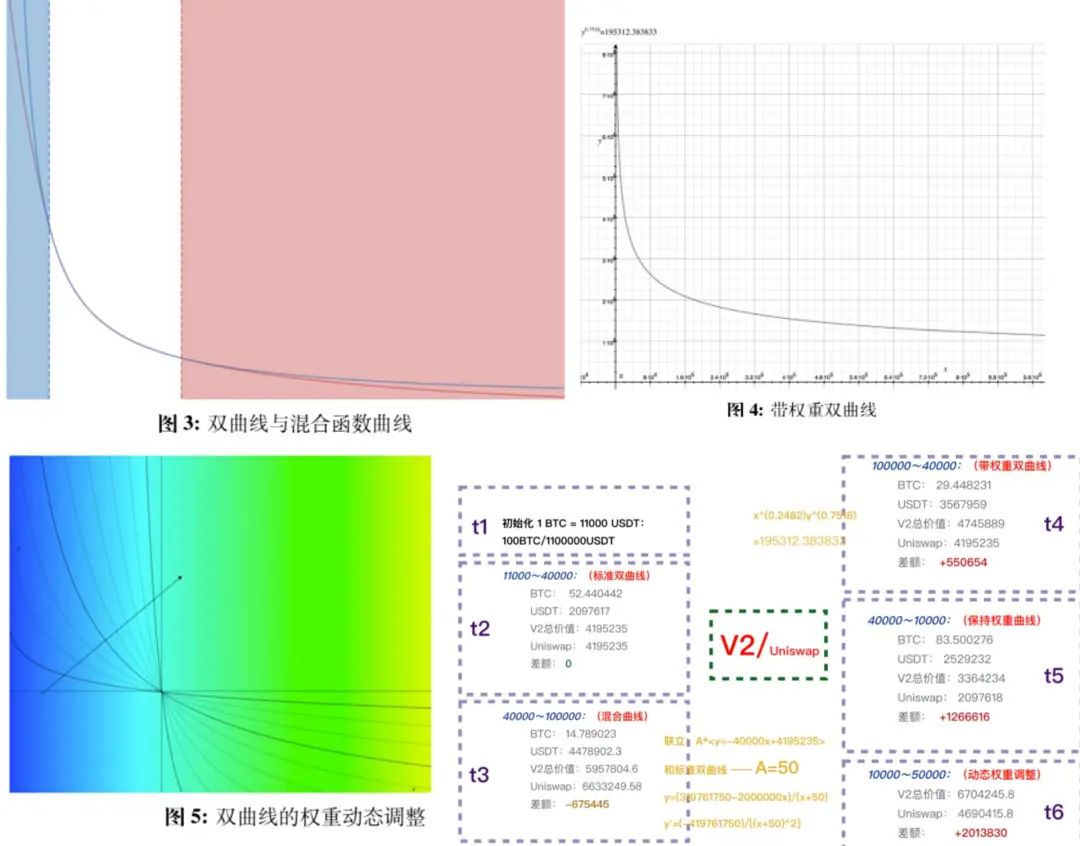
這種解決方案的優勢是一旦策略預測成功,不僅可以解決無常損失,還可以大幅度幫助LP 獲得基金級別的財富增值,這是市面上任何AMM 都給不了的,即便是有流動性挖礦加持。而且這種策略不依賴任何外部因子,只依賴自身策略,因此不會引入其他風險,即便是後市行情不如所願,也可以提前更改下一個函數切換點,及時改變下一段函數形態,避免大規模損失。缺陷也是十分明顯的,即需要非常專業的基金經理預判和策略,需要能夠預測好較大範圍的後市行情,而且分段函數的構造十分複雜,超導V2 在構建自身策略時,其實是有更好的函數構造,但迫於數學形態過於復雜且工程實現困難,便選擇瞭如上實現案例,也是一種折中辦法。
4 經濟補償
這一類是最為大家熟悉的方法,即以自身代幣的形式為LP 補償損失,包括Bancor V2.1 和流動性挖礦兩種形式。
Bancor V2.1 是在Bancor 意識到Bancor V2(如上第一類)無法解決無常損失而且會帶來預言機系統風險之後重新制定的無常損失方案,這種方法會從系統層面記錄每一個LP 初始做市時的倉位,在無常損失發生後,會通過系統增發Bancor 代幣來補償無常損失。
流動性挖礦也是異曲同工,不過Bancor V2.1 的補償更為精細,有多少損失便補貼多少自身代幣。而市面上的流動性挖礦,多則APY 可達幾十倍,少則也有兩三倍,是一場瘋狂的造富運動,即便是LP 參與了一個月,所獲得的挖礦財富也足夠其應對無常損失的任何上限。
因此流動性挖礦如果可以做好“善後”工作,也未嘗不是一種根本性的無常損失解決方案。
5 期權對沖
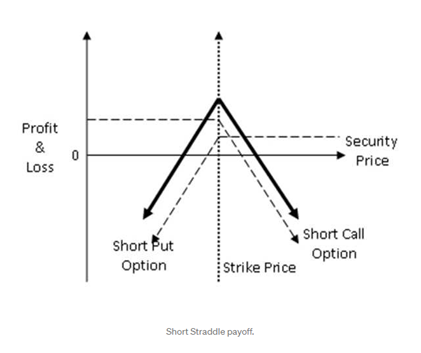
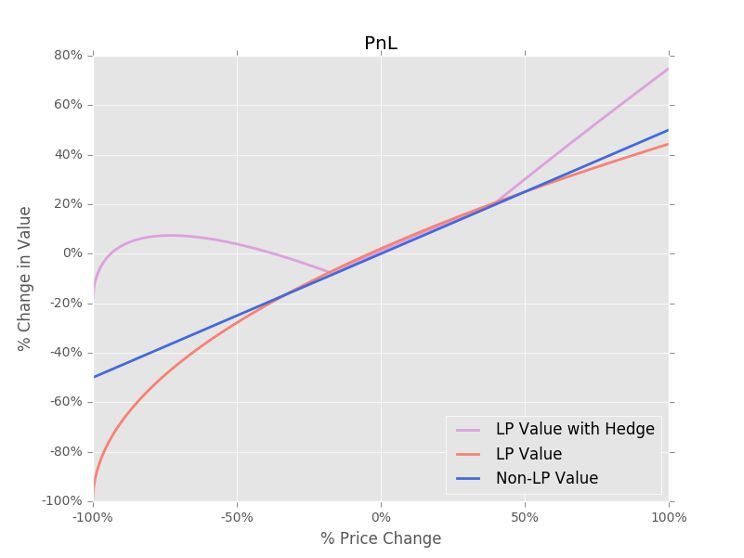
也叫Hedge,這一類研究非常稀少,幾乎不見於任何市面上的項目,之前火幣研究院有過一篇專門的報告(AMM做市無常損失對沖分析系列一:損益及期權對沖模型構建https ://zhuanlan.zhihu.com/p/260141168)。火幣研究院的文章論證了通過看跌期權來補償無常損失的基本結論,並給出了具體數量和位置指導,一定程度上是可以明顯起到緩解無常損失的作用,見下圖。
後來我們也發掘了幾篇非常好的行業論文,尤其是Placeholder 的研究員Alex Evans 的研究工作(論文When does the tail wag the dog? Curvature and market making 和論文Liquidity Provider Returns in Geometric Mean Markets)十分突出,我們也在此對其進行簡單解讀。
在傳統金融理論中,動態套期保值是機構投資者利用股指期貨或股票與無風險資產創造合成的看跌期權並通過使用合成看跌期權策略尋求保護投資組合價值的策略。而在CFMM 機制下,有人提出可以類比資產的Delta 值(δ)和Gamma(γ)值來規避高額LP 風險。接下來我們將會計算LP 的動態對沖數量,並展示它們如何在交易中表現良好。通過以下的數學推導,我們還可以看出動態對沖數量和曲率之間的關係。
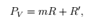
儲備的投資組合價值其中m 為市場價格,R 和R' 儲備金數額,則我們可以得到 。
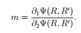
如何證明此等式的正確性? 函數ψ 只與R 和R' 有關,在無套利的情況下,市場價格m 滿足。則等式滿足函數ψ 對市場價m 求一階導為零,帶入得:
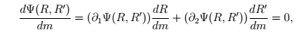
整理即得:
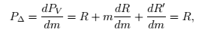
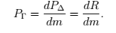
在Joseph Clark 所著的論文《The replicating portfolio of a constant product market》中,他提出了用帶CPM 收益的歐式期權來提高LP 的收益。在他看來,LP 根據新的資產比例得到的一定比例的交易費用可以被精確複製與期貨和期權的靜態組合。如果這些期貨和期權存在並且是可交易的,每千次展示費用收取的交易費用將由期權價格決定和預期的交易量。如果期貨和期權不存在,則CPM 的收益可以用來創建它們。
我們可以詳細討論下在CPM 模式下的收益以及最終組合投資的總收益。
我們假定當前市場價為 ,則此時準備金可以表示為。那麼在時間t 內我們得到的組合投資淨利潤為 。顯然,我們可以得到最終投資的總收益為。
當然,我們還有另外一種思路,就是研究在CPM 模式之下複製歐洲看漲期權對LP 的收益,跟前文說的組合收益不同,這種期權不是靜態的,但是它可以做到在有限的套期保值下保持精確。仿照期權Greeks,Joseph Clark 給出了在CPM 模式之下,影響期權價格的各項指標:

複製期權的總回報等於CPM收益和期貨的原有收益相加:
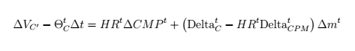
綜上我們不難看出,Joseph Clark 認為可以用靜態資產組合來對沖LP 的風險損失,而動態對沖數量和曲率有密切聯繫。若期權和期貨不可交易,那麼CPM 帶來的收益也可以作為複制期權的備選項。
未完待續
我們還有很多課題和最新研究成果與大家分享,包括
(1)LP 終極收益的數學公式表達以及影響LP 收益的最本質因子,其實都可以通過公式論證出來,以幫助AMM 產品更好的進行迭代改進,例如影響LP 收益的有曲率、informed trading 等;
(2)流動性挖礦(Yield Farming)的真正使命,除了補償無常損失外,還可以起到非常好的AMM 項目自身原始代幣的發行以及代幣價格穩定的作用,我們認為通過流動性挖礦發行的自身代幣價格,不會存在死亡螺旋的現象,反而會造就項目市值的一個強支撐,當然前提是該項目是非常有人氣有口碑的項目,此外,流動性挖礦的具體補貼數值也存在數學表達和影響因子;
(3)AMM 項目在未來會都向著動態AMM 形態發展,即不再局限於一條曲線形態,會根據不同的情境輔助以多種曲線形態;曲率是一個被大大忽略的曲線研究領域,曲率幾乎決定著一切AMM 產品特徵,曲率甚至可以改變一個新幣種的主市場定價問題。