助推谷歌衝擊4兆的TPU，如何在區塊鏈領域大顯身手？

作者： Eli5DeFi

編譯：Tim，PANews

PANews編按：11月25日，Google總市值創歷史新高，達3.96兆美元，助推股價的因素除了新發布的最強AI Gemini 3，還有其自研晶片TPU。除了AI領域外，TPU在區塊鏈也將大顯身手。

現代計算的硬體敘事基本上是由GPU的崛起所定義的。

從遊戲到深度學習，英偉達的平行架構已成為業界公認的標準，使得CPU逐漸轉向協管角色。

然而，隨著AI模型遭遇規模化瓶頸、區塊鏈技術邁向複雜密碼學應用，新的競爭者張量處理器（TPU）已然登場。

儘管TPU常被置於GoogleAI戰略的框架下討論，但它的架構卻意外契合區塊鏈技術的下一個里程碑後量子密碼學的核心需求。

本文透過整理硬體演進歷程、比較架構特性，闡釋為何在建構抗量子攻擊的去中心化網路時，TPU（而非GPU）更能勝任後量子密碼學所需的密集型數學運算。

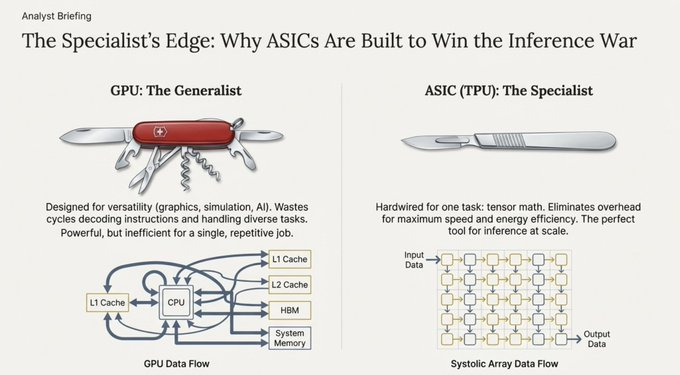
硬體演進：從串列處理到脈動架構

要理解TPU的重要性，就需要先了解它所解決的問題。

中央處理器（CPU）：身為全能型選手，擅長串列處理與邏輯分支操作，但在需要同時執行海量數學運算時則作用有限。
圖形處理器（GPU）：身為平行處理專家，設計初衷是渲染像素，因而擅長同時執行大量相同任務（SIMD：單指令多資料流）。這項特性使其成為早期人工智慧爆發的中流砥柱。
張量處理器（TPU）：作為專業型晶片，由Google專為神經網路運算任務設計。

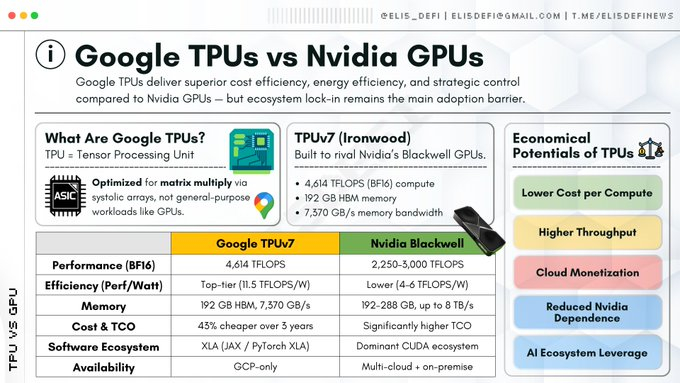
脈動架構優勢

GPU與TPU的根本差異在於它們的資料處理方式。

GPU需重複調取記憶體（暫存器、快取）進行運算，而TPU則採用脈動架構。這種架構如同心臟泵血般，使資料以規律脈動的方式流經大規模計算單元網格。

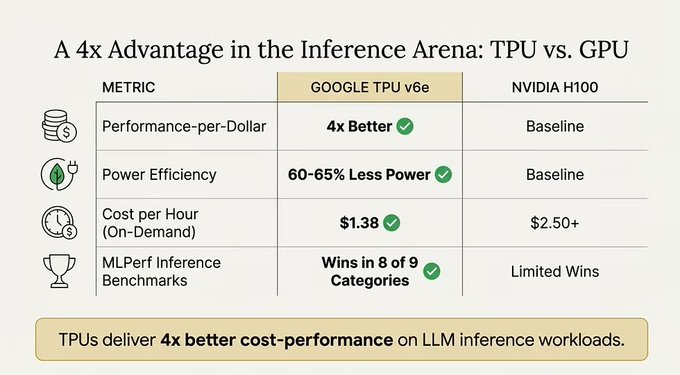
https://www.ainewshub.org/post/ai-inference-costs-tpu-vs-gpu-2025

計算結果直接傳遞至下一計算單元，無需寫回記憶體。這種設計極大緩解了馮諾依曼瓶頸，即資料在記憶體與處理器間反覆移動產生的延遲，從而在特定數學運算上實現吞吐量的數量級提升。

後量子密碼學的關鍵：為何區塊鏈需要TPU？

TPU在區塊鏈領域最關鍵的應用並非挖礦，而是密碼學安全。

目前區塊鏈系統所依賴的橢圓曲線密碼學或RSA加密體系，在應對Shor演算法時存在致命弱點。這意味著一旦出現足夠強大的量子計算機，攻擊者就能從公鑰反推出私鑰，足以徹底清空比特幣或以太坊上的所有加密資產。

解決之道在於後量子密碼學。目前主流的PQC標準演算法（如Kyber、Dilithium）都是基於Lattice密碼學建構。

TPU的數學契合性

這正是TPU相較GPU的優勢。 Lattice密碼學嚴重依賴大型矩陣和向量的密集操作，主要包括：

矩陣-向量乘法：As+e（其中A為矩陣，s和e為向量）。
多項式運算：基於環的代數操作，通常運用數論變換實現。

傳統GPU將這些運算視為通用平行任務處理，而TPU則透過硬體層級固化的矩陣運算單元實現專屬加速。 Lattice密碼學的數學結構，與TPU脈動陣列的物理構造幾乎形成嚴絲合縫的拓樸映射。

TPU與GPU的技術博弈

儘管GPU仍是業界通用的萬能王者，但在處理特定數學密集任務時，TPU具有絕對優勢。

結論：GPU勝在通用性與生態系統，而TPU則在密集線性代數計算效率上佔優勢，而這正是AI與現代先進密碼學所依賴的核心數學運算。

TPU拓展敘事：零知識證明與去中心化AI

除後量子密碼學外，TPU在Web3另兩大關鍵領域也展現出應用潛力。

零知識證明

ZK-Rollups（如Starknet或zkSync）作為以太坊的擴容方案，其證明生成過程需要完成大量計算，主要包括：

快速傅立葉變換：實現資料表示形式的快速轉換。
多標量乘法：實現橢圓曲線上的點運算組合。
FRI協定：驗證多項式的密碼學證明系統

這類運算並非ASIC擅長的雜湊計算，而是多項式數學。相較於通用CPU，TPU能顯著加速FFT與多項式承諾運算；而由於這類演算法具有可預測的資料流特性，TPU通常比GPU能實現更高效率的加速。

隨著Bittensor等去中心化AI網路的興起，網路節點需具備運行AI模型推理的能力。運行通用大語言模型本質上就是在執行海量矩陣乘法運算。

相較於GPU集群，TPU能使去中心化節點以更低能耗處理AI推理請求，從而提升去中心化AI的商業可行性。

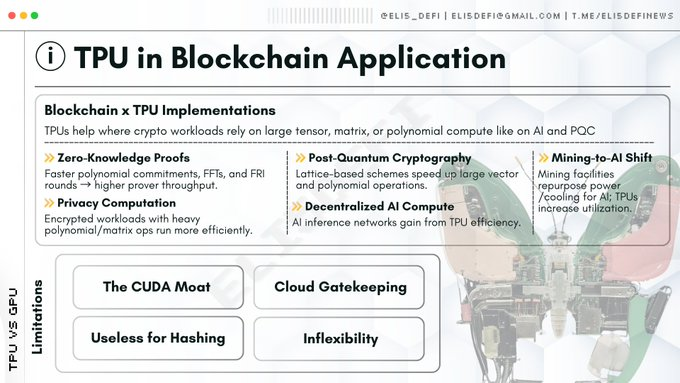
TPU生態版圖

儘管目前多數項目因CUDA的普及性仍依賴GPU，但以下領域在TPU整合方面蓄勢待發，尤其在後量子密碼學與零知識證明的敘事框架下極具發展潛力。

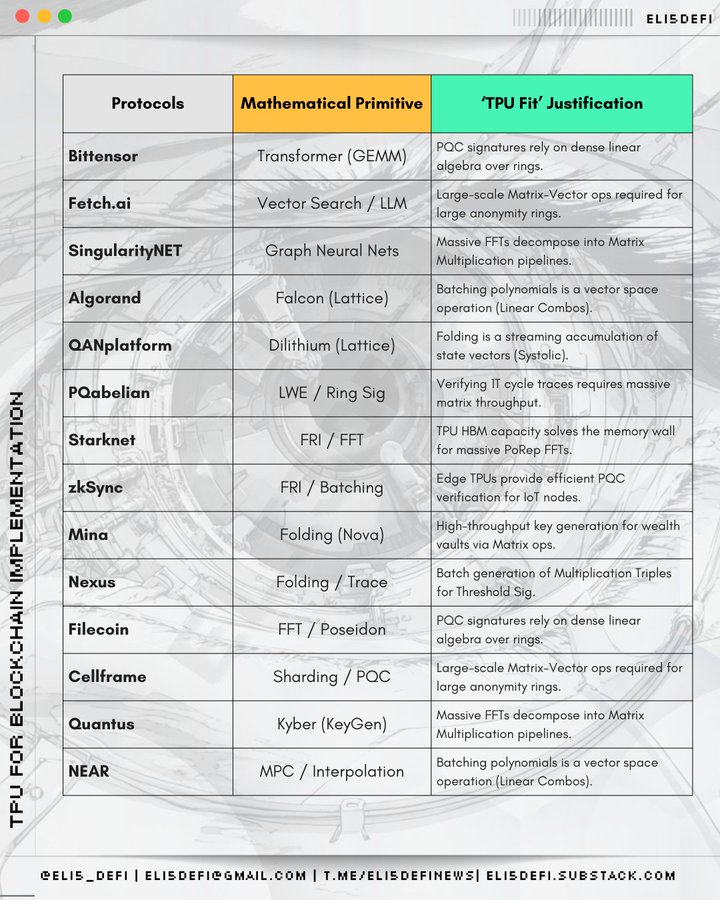
零知識證明與擴容方案

為何選擇TPU？因為ZK證明產生需要大規模並行處理多項式運算，而在特定架構配置下，TPU對此類任務的處理效率遠超通用GPU。

Starknet（二層擴容方案）：STARK證明嚴重依賴快速傅立葉變換和快速里德-所羅門互動預言證明，這些運算密集型操作與TPU的運算邏輯高度契合。
zksync（二層擴容方案）：它的Airbender證明器需處理大規模FFT與多項式運算，這正是TPU能破解的核心瓶頸所在。
Scroll（二層擴容方案）：它採用Halo2與Plonk證明體系，其核心運算KZG承諾驗證與多標量乘法能完美匹配TPU的脈動架構。
Aleo（隱私保護公鏈）：專注於zk-SNARK零知識證明生成，其核心運算依賴的多項式數學特性與TPU的專用計算吞吐量高度契合。
Mina（輕量級公鏈）：採用遞歸SNARKs技術，其持續重新生成證明的機制需重複執行多項式運算，此特性使得TPU的高效計算價值凸顯。
Zcash（隱私幣）：經典Groth16證明體係依託多項式運算。雖屬早期技術，但高吞吐量硬體仍能使其顯著獲益。
Filecoin（DePIN、儲存）：它的複製證明機制透過零知識證明與多項式編碼技術，驗證儲存資料的有效性。

去中心化AI與代理型計算

為何選擇TPU？這正是TPU的原生應用場景，專為加速神經網路機器學習任務而設計。

Bittensor：其核心架構是去中心化AI推理，這與TPU的張量運算能力形成原生的精準契合。
Fetch（AI代理）：自主AI代理依賴持續的神經網路推理進行決策，而TPU能以更低延遲運行這些模型。
Singularity（AI服務平台）：作為人工智慧服務交易市場，Singularity透過整合TPU顯著提升了底層模型執行的速度與成本效益。
NEAR（公鏈、AI策略轉型）：向鏈上AI與可信賴執行環境代理的轉型，它所依賴的張量運算正需TPU加速實現。

後量子密碼學網絡

為何選擇TPU？後量子密碼學的核心運算常涉及格中最短向量問題，這類需要密集矩陣與向量運算的任務，與AI工作負載在運算架構上具有高度相似性。

Algorand（公鏈）：採用量子安全哈希與向量運算的方案，與TPU的平行數學運算能力高度契合。
QAN（抗量子公鏈）：採用Lattice密碼學，其底層所依賴的多項式、向量運算，與TPU專精的數學最佳化領域具有高度同構性。
Nexus（計算平台、ZkVM）：它的抗量子運算準備工作涉及的多項式與格基演算法，能高效地映射到TPU的架構上。
Cellframe（抗量子公鏈）：採用的Lattice密碼學與雜湊加密技術涉及類張量運算，使其成為TPU加速的理想候選方案。
Abelian（隱私代幣）：專注後量子密碼學Lattice運算。與QAN類似，其技術架構能充分受益於TPU向量處理器的高吞吐量特性。
Quantus（公鏈）：後量子密碼學簽章依賴大規模向量運算，而TPU處理此類運算的平行化能力遠超標準CPU。
Pauli（運算平台）：量子安全運算涉及大量矩陣運算，而這正是TPU架構的核心優勢。

發展瓶頸：為何TPU尚未全面普及？

若TPU在後量子密碼學與零知識證明領域如此高效，為何產業仍在搶購H100晶片？

CUDA護城河：英偉達的CUDA軟體庫已成為業界標準，絕大多數密碼學工程師都基於CUDA進行程式設計。若要將程式碼移植到TPU所需的JAX或XLA框架，不僅技術門檻高，還需投入大量資源。
雲端平台進入門檻：高階TPU幾乎被Google雲端獨家壟斷。去中心化網路若過度依賴單一中心化雲端服務商，將面臨檢討風險與單點故障危機。
架構僵化：密碼學演算法若需微調（如引入分支邏輯），TPU效能會急遽下滑。而GPU處理此類非規則邏輯的能力遠勝TPU。
哈希運算中的限制：TPU無法取代比特幣礦機。 SHA-256演算法屬於位元級運算而非矩陣運算，TPU在此領域毫無用武之地。

結論：分層架構是未來

Web3硬體的未來並非一場贏家通吃的競爭，而是正朝著分層架構的方向演進。

GPU將繼續承擔通用運算、圖形渲染及需處理複雜分支邏輯任務的主力角色。

TPU（及同類ASIC化加速器）將逐步成為Web3"數學層"的標準配置，專門用於產生零知識證明與驗證後量子密碼學簽章。

隨著區塊鏈向後量子安全標準遷移，交易簽章與驗證所需的海量矩陣運算將使TPU的脈動架構不再是可選項，而成為建構可擴展的量子安全去中心化網路的必備基礎設施。