作者： Stephen Perrenod , 技術分析師

編譯：Felix, PANews

比特幣史上最大的泡沫（多頭市場）分別出現在2011 年、2013 年、2017 年和2021 年。儘管許多比特幣投資者堅信四年一個週期，但2025 年並未出現泡沫。

為什麼？因為大家被「泡沫以線性時間、每四年一次」的敘事洗腦了，都預計在2012 年、2016 年、2020 年和2024 年這四個減半年份之後會出現高峰。這種敘事也因美國的商業週期和總統選舉年而進一步強化。

個人也曾深陷四年線性週期的假設中。

過去一年，個人越來越專注於泡沫建模，把「核心冪律區」（長期趨勢）和「泡沫區」（短期偏離）分開分析。

結果越來越清楚：泡沫的「能量」正在衰減，大致上與比特幣「年齡」成反比，或說以年齡的-0.83 次方衰減。

大家還錯誤地以為每次泡棉的百分比漲幅會一樣大，其實泡棉強度明顯在衰減。而本文研究也表明，泡沫在時間上的間隔也在拉長。

那2011 年的泡沫呢？大家習慣把2011 年的大泡沫當作「早期異常」直接忽略。但2011 年的泡沫其實和2013 年、2017 年一樣重要，理應同等對待。如果泡棉並非以線性週期出現，而是以對數週期出現呢？這種現象稱為對數週期行為。

對數週期泡沫源自於冪律

畢竟，比特幣本身就是一個冪律資產，其隨時間的走勢具有尺度不變性（scale invariance）。要價格漲幅相同，就必須有相同比例的時間成長。例如，如果價格與年齡的關係為Price ~ Age^k，那麼以美元計算，如果k = 5.7，當年齡翻倍時，價格將增加52 倍。要實現價格同樣52 倍的增長，比特幣的年齡就需要從2 年增長到4 年，然後從4 年增長到8 年，再從8 年增長到16 年，以此類推。

因此，泡沫的出現間隔越來越長也就不足為奇。一個對數時間區間可能只對應一次大泡沫，線性時間的間隔會越來越長。

事實上，早在2019 年，Giovanni Santostasi（第二次減半前就發現比特幣冪律性質的人）就提出了圍繞冪律趨勢的對數週期模型（圖1中那條彎曲/振盪的線）。它幾乎對應了2011、2013、2017 三次泡沫，甚至預測下一次泡沫高峰在x=3.817 處（即10^3.817 ≈ 6561天，約18 年），也就是2026 年底到2027 年初。

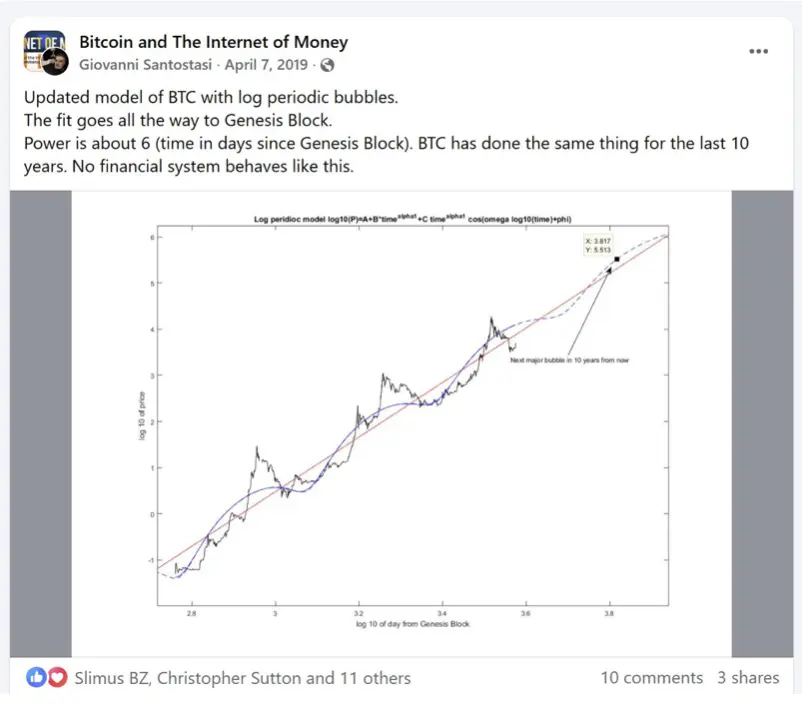
圖1

這篇六年前的貼文應該被更多人點贊，雖然振幅擬合一般，但時間點非常準，後面會看到第四個峰值的預測可能極其準確。

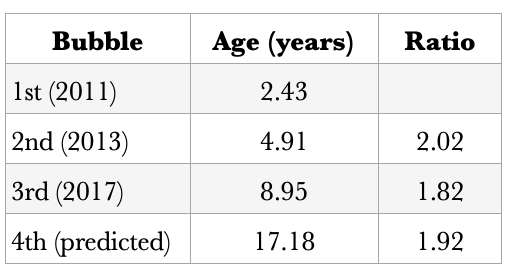
粗略觀察年齡比率。前兩個相鄰的大泡沫之間的比率分別為2.02 和1.82，取平均1.92，第四次泡沫大約在年齡17.18 年（2026 年初）。當然，這只是粗略的初步猜測。

無論是Giovanni 的擬合模型，還是本人在其基礎上增加6 年半的資料後運行的模型，都沒有預測到2021 年或2025 年會出現泡沫。這就引出了一個問題：2021 年的雙泡沫究竟​​是基本面泡沫還是其他原因造成的泡沫？

完整的對數週期分析

接下來要注意的是，完整的對數週期演算法（full log-periodic algorithm）比僅使用兩個峰值之間的間隔進行分析要精確得多。

它與地球物理學家Didier Sornette 推廣的一種更複雜的對數週期分析有關，該分析最初用於地震、其他自然現像以及金融時間序列。完整的方程式包含七個參數，其中包括一個局部冪律指數（local power law index）和一個帶有對數時間依賴的諧波（餘弦）項。

在本文中，將對完整價格歷史記錄的對數時間進行傅立葉和小波分析。以黃金盎司為單位衡量比特幣，進行了尺度不變性測試。在以10 為底的對數價格殘差中，冪律指數為5.30，R²為0.94，標準差為0.314。

將移除5.30 指數冪律後的壓縮殘差進行對數時間傅立葉轉換分析，得出對數週期特徵波長參數λ = 2.07。在上述提到的峰值區間公式中，這大致對應於各泡沫之間「年齡」的比率，但它是一個更全局的估計，同時也考慮了諧波。小波分析發現λ 的範圍在2.00 到2.10 之間。

最終確定的最佳擬合λ 值對應於基模（fundamental mode），它很好地擬合了2011、2013 和2017 年的泡沫。同時它預測2017 年後的第一個基模泡沫將出現在18.4 年，即2027 年5 月下旬。如果取小波分析的下限λ=2.0，則預測年齡為17.9 年，也就是大約一年後（2026 年底），這與Giovanni 在2019 年的預測非常接近。

「離散年齡比率模型和你的LPPL 擬合描述的是相同的底層離散尺度不變性（λ≈2），只不過坐標係不同；一旦你把ln(t_c − t) 與年齡t、噪聲以及半諧波考慮進來，二者是完全一致的，都指向第四個基模泡沫出現在2026—2027 年左右，其中PL202020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202027/2/2027 年：2027 年：2027 年 2027 年的約距泡沫模型。年），而粗略的年齡比率法偏向稍早（約2026 年）。

2021 年的泡沫算什麼？

在這一框架下，2021年並不是基模，而是基模的第一次諧波（頻率更高，但波長更短，因為在LPPL 模型中，對數週期行為的角頻率滿足λ = e^{2π/ω}）。這對應的比率是2.07 的平方根，即1.44。8.95 × 1.44 = 12.89 歲，正好對應2021 年底，與實際雙頂泡沫時的年齡12.85 年高度吻合。

2025 年呢？在對數週期序列中，並沒有預測會出現泡沫。今年比特幣相對黃金表現疲軟，恰恰符合這個框架的預期。

圖2 顯示了基頻和半諧波（頻率上為一次諧波，波長上稱為半諧波）模式的完整映射。紅色垂直線代表基頻模式的泡沫峰值，藍色線代表半諧波。三條紅線吻合得非常好，但藍色線也很好地反映了該諧波的較小泡沫。這並非完整的映射，還有更高次的諧波，但貢獻較小。

第四條紅色線對應年齡18.4 年的預測，即下一次比特幣相對黃金的大泡沫。比特幣可能從2026 年初開始以黃金計價上漲，並在2027 年第二季見頂。

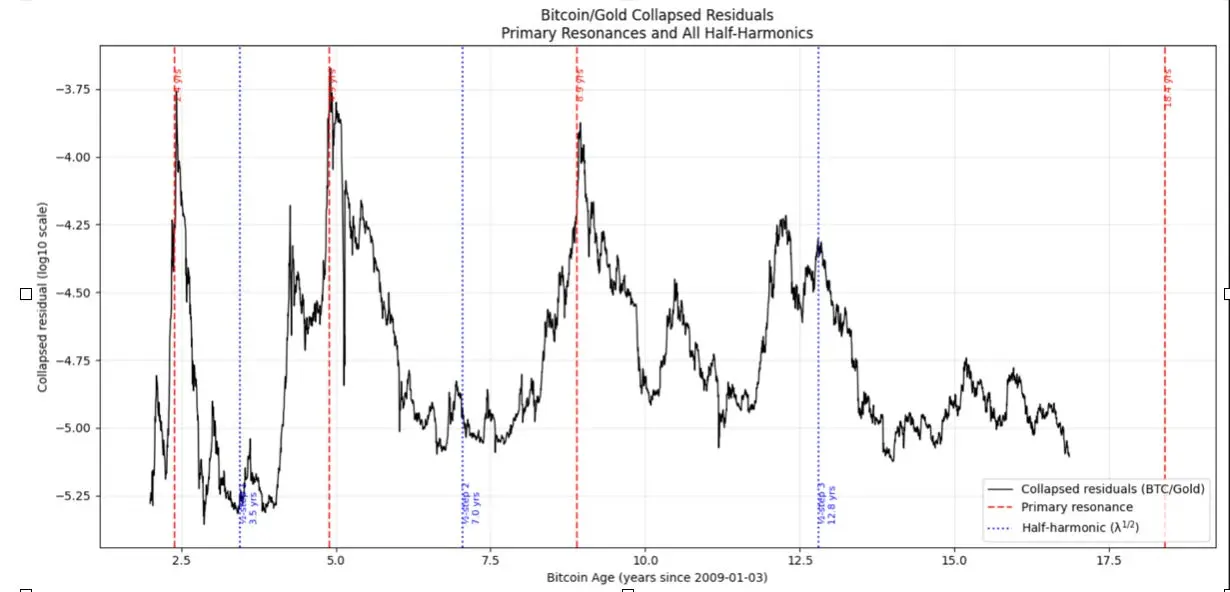
圖2

為何會有這種行為？連續尺度不變性+ 離散尺度不變性。

要理解比特幣的價格走勢，必須同時理解連續尺度不變性和離散尺度不變性。連續尺度不變性就是讀者早已熟悉的長期冪律趨勢。而離散尺度不變性對應間歇性泡沫，可用LPPL（對數週期冪律）模型來描述。因為名稱中帶有“對數週期冪律”，容易產生混淆。

LPPL 模型適用於中短週期金融序列，在本例中，專門用來模擬偏離核心冪律趨勢的那些大幅波動。因此同時有兩種情況：即整體的冪律趨勢（連續的），以及在其之上發生的高波動性偏離（離散的）。

從長期來看，比特幣的採用率遵循Metcalfe 定律呈現冪律增長。

泡沫的產生是由於新參與者在比特幣價格突破新的數量級時（比特幣價格在其短暫但影響巨大的歷史中已上漲超過7 個數量級，即7 個10 倍）產生興趣而引發的參與熱潮。

當比特幣能改變你（或機構）的命運時，它才會被採用。

早期價格低時，主要吸引密碼朋克愛好者、散戶交易和投資；隨著時間推移，吸引了越來越高級別的機構資本：先是礦工，然後是交易所、期貨交易，之後是一些上市公司，再到現在的主權財團公司、ETF 等機構工具。現在機構資本是淨買方，而且它們的持股大多是為大量客戶和股東託管的。

當比特幣的價格和市值夠高時，退休金、主權財富基金，甚至國家金庫都會被誘使投資。每一次後續泡沫在黃金盎司計價的水平上都遠高於前一次（在法幣計價下更高），隨之，大量新資本大規模地採用比特幣。

即使市值達到2 兆美元，比特幣對大型企業和中大型國家的財政部來說仍太便宜，不足以產生顯著影響。即便他們能以大約1000 億美元的價格購買100 萬枚比特幣，也不會「改變他們的命運」。

比特幣的冪律效應推動著規模越來越大的參與者湧入市場。這種效應源自於其協議本身：吸引算力、增強安全性、先行者優勢等，這些因素最終必然會推高價格。

因此，法定貨幣被激勵流向比特幣，甚至原本可能流向黃金的法定貨幣也轉而流向了比特幣。沒錯， 2025 年比特幣的表現相對黃金而言較為疲軟，但根據上述分析，這很可能是比特幣相對於黃金的一個低谷年份。

新一輪更大玩家的採用浪潮以LPPL 泡沫的形式到來，這意味著它們必須在其局部臨界時間點崩潰。因此，價格軌跡會回歸到長期冪律。

由於冪律關係為P ~ T^k，其中k 為指數，T 為年齡，且其一階導數為δP / P ~ k/T，因此泡沫的間距預計呈對數關係。相對成長率隨比特幣年齡的倒數而降低，但泡沫的出現需要δP / P >> k/T。根據定義，當價格成長速度遠高於長期冪律趨勢時，就形成了泡沫。

此表達式可以改寫為δ (log P) ~ k * δ (logT)，因此可以預期，對數價格的大幅波動（較大的乘法比率）需要越來越長的線性時間，也就是說，它們需要對數時間按比例增加，其量級為所需乘法波動的1/k 次方根。

事實上，以黃金價格計算，2011 年、2013 年和2017 年泡沫的峰值中位數相對於冪律趨勢是10.1 倍，冪律指數為5.31。預計λ 約為10.1^(1/5.31) = 1.55，大約是峰值時間對數週期擬合所得值2.07 的四分之三。因此，根據經驗，以黃金價格計算時，λ ~ (4/3) F^(1/k)，其中F 是峰值與冪律趨勢價格的典型比率。

總結

比特幣的主要價格走勢由以下兩個面向組成：

• 連續尺度不變性可以用冪律表示，以黃金計價的指數約為5.3，以美元計價的指數約為5.7。
• 離散尺度不變性（DSI）體現在間歇性的泡沫事件中，因為只有當價格和市值達到足以吸引新資本且監管環境允許的水平後，規模更大的新資本層級就會採用比特幣。這些離散尺度不變事件可以用LPPL 模型來描述泡棉及其隨後的崩盤。

2013 年泡沫以散戶、早期礦工、早期比特幣創業公司和第一代交易所為主。 2017 年的泡沫則吸引了對沖基金、家族辦公室和其他高淨值人士的參與，而GBTC 交易早在2015 年就開始了。泡沫的頂峰出現在2017 年12 月芝加哥商品交易所(CME) 期貨推出之後，使得高效的做空和對沖成為可能。 2021 年的泡沫得到了部分企業財務部門和一些小型政府機構的認可。由於機構參與度和相關機制的加強，對沖和做空的能力也更強，導致泡沫最終破裂，價格也得以像彈簧一樣回歸冪律趨勢。

下一輪大規模採用浪潮可能集中在2026 年和2027 年，屆時比特幣市值預計將接近5 兆美元，並吸引大型企業、主權財富基金以及政府（國家退休基金和國家財政部）的長期配置。比特幣的階段性泡沫反映了全球資本的不同層級：從散戶到基金，再到企業，最後到主權國家，這導致了DSI 行為以及與市值和機構參與度增加相關的波動性下降。

「每一層級資本只有在比特幣規模足夠大、足夠流動、足夠可信時才會被解鎖​​——由於其收益呈冪律增長和k/t衰減，這個過程需要的時間越來越長。」— ChatGPT 5

DSI 的基模波長參數λ = 2.07（對數時間），大致對應泡棉間隔的兩倍。 2017 年泡沫是最後一個基模，2021 年是第一次諧波，2025 年在本框架下預期不會出現泡沫。下一輪以黃金計價的比特幣高峰預計在2026 年第四季（小波分析最低值）至2027 年第二季（傅立葉分析值）之間出現。

相關閱讀：牛還是熊？ 5大訊號主導比特幣新周期