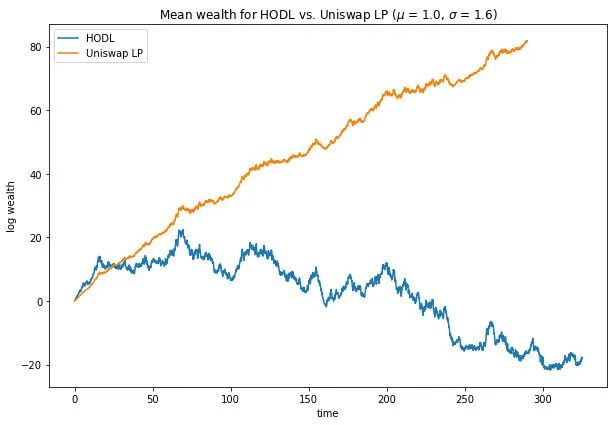
Uniswap LP“被迫”致富
1 問題
10月14日,Charlie Noyes在Twitter上發布了一個他和Dan Robinson一直在辯論的問題:對於任何Uniswap的交易對,最佳費用是多少?這種最佳費用能否超過未重新平衡的投資組合實現“無暫時性虧損”甚至是超預期的增長?
1.1 基礎規則
自動化的做市商AMM是一種去中心化的交易機制,可以讓用戶在交易像USDC、ETH等的鏈上資產。
Uniswap是以太坊上最受歡迎的AMM。像大多數AMM一樣,Uniswap通過持有兩種資產的儲備來實現交易對之間的兌換。並儲備量確定交易價格,使價格與大盤保持一致。
為“資金池”提供流動性的人稱為“LP”,LP為其他用戶提供了流動資產以進行交易。 LP需要同時注入兩種資產,承擔了交易風險以換取一部分Uniswap的收益。
1.2 問題設定
問題在於,資金池是在資金和另一種價格會隨機波動的資產之間提供流動性。更殘酷的假設是,所有的交易幾乎都是套利交易—只有當AMM的價格超出市場水平時才會發生。
換句話說,每筆交易都會導致資金池中的資金虧損。
1.3 一般情況
乍一看,這種情況會成為Uniswap的LP的代價高昂的錯誤。
因為做市商要求的買入價低於賣出價,所以當資產價格不動時,做市商直接獲利,他們得到的買入和賣出量大致平衡。這些交易通常被稱為“不知情”交易,因為它們與短期價格變動沒有關聯。
另一方面,做市商在價格下跌之前買入,或在上漲之前賣出,都會虧損。因此,做市商最擔心的交易對手之一就是套利者,套利者只有在價格發生變化時才進行交易。套利者的每筆交易對其來說都是純利潤,對於做市商來說則純虧損。
由於Uniswap中沒有不知情的交易(實際上每筆交易都是套利交易),因此LP顯然會損失慘重。
甚至可以懷疑,對於一些潛在的價格波動,作為Uniswap的LP在每一筆交易中都會被套牢。
2 解決方案
如果一項資產相對於其平均回報率的波動性足夠高,那麼隨著時間的推移,Uniswap上的LP將比HODLer收益更好,即使進場的只有套利交易。
這是由於一種稱為“波動性收益”的現象造成的:在某些條件下,通過週期性地對兩種資產進行再平衡,它們的表現有可能超過任何靜態投資組合。在這種情況下,“再平衡”是指通過交易使每項資產中持有的比例返回到固定的50/50。
因此,當他們被套利時,LP會向市場支付一筆費用,為他們重新平衡投資組合。在這個特殊的數字設置中,這種再平衡是有益的,可以希望盡可能多地這樣做。這意味著LP應將其費用(決定發生再平衡的價格敞口)設置為盡可能低而不為零。
這對於Uniswap來說是個好消息,因為這意味著即使在套利交易占主導的情況下,低費用仍然是有意義的,這使Uniswap在鏈上訂單不斷增加並開始提供更小的價差時保持競爭力。
也就是說,值得強調的是,這些結果適用於非常特殊的程式化數字設置,其中涉及的假設與Black-Scholes期權定價模型的假設非常相似。
2.1 比較標準
我們通過比較不同策略的“漸近財富增長率”來評估它們,這些“漸進財富增長率”衡量了它們在很長一段時間內增值(或貶值)的速度。
我們將所有策略與“非再平衡投資組合”進行比較,“非再平衡投資組合”一半是現金形式,一半是持有風險資產形式,並保持不變。這意味著,在最壞的情況下,當風險資產喪失其全部價值時,“非再平衡資產組合”將幾乎全部由現金組成,從長遠來看其增長率為零。另一方面,如果風險資產呈指數增長,它將很快在“非再平衡投資組合”中佔據主導地位,因此其增長率與風險資產相同。
值得注意的是,兩種資產可以共享相同的“漸近財富增長率”,但表現的差異也很大。例如,如果風險資產的增長率為零,那麼享有零手續費的Uniswap價值將始終低於“非再平衡投資組合”,但由於預期兩者都不會隨著時間複合增長或虧損,兩者的財富增長率都將為零。
2.2 波動阻力
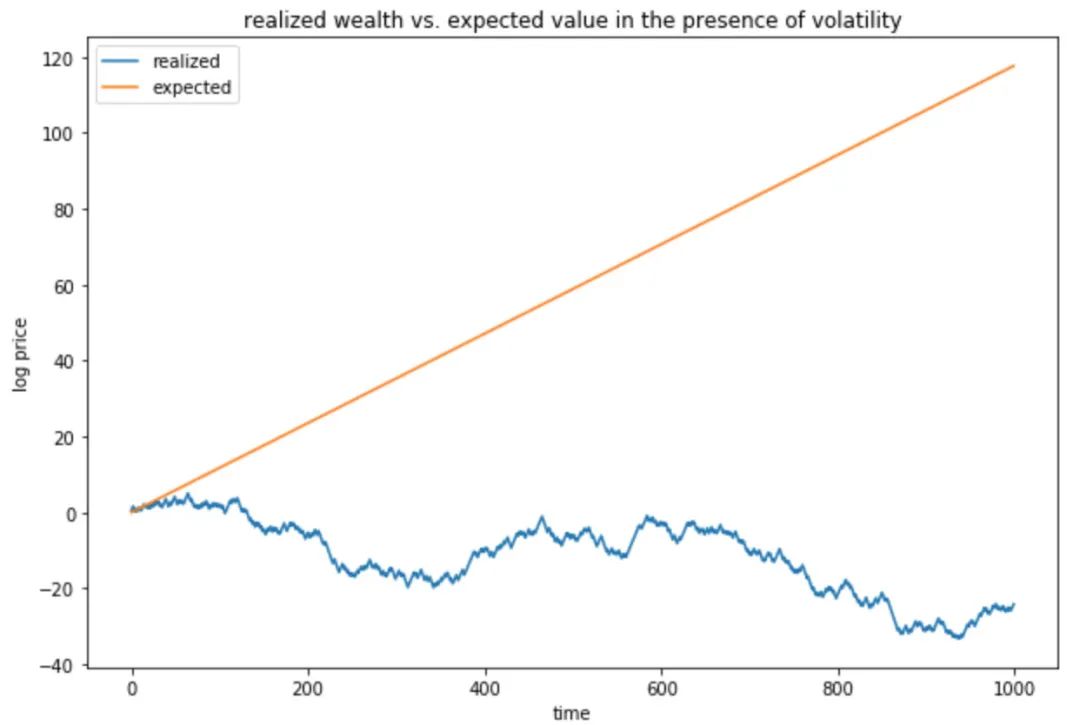
波動阻力對於50%損失/ 75%收益的作用過程
要理解這些結果,首先要理解波動阻力的概念。假設每年我們的風險資產價格要么下跌75%要么上漲50%,兩者發生的概率相等。
在任何特定年份,如果我們投資$100,“期望值”是50/2+175/2=$112.5。如果只是購買並持有,投資組合預期將每年增加12.5%—這似乎是一筆不錯的交易。
不幸的是,在現實世界中,我們的利潤其實無法實現。如果我們購買並持有此組合,最終將失去一切。這是因為,隨著時間的流逝,財富增加將帶來巨大的損失。
如果第一年損失50% ,第二年增值75% ,第二年期末餘額將只有50%∗175%=87.5%。同樣,如果第一年收益75%,第二年虧損50%,第二年期末餘額依舊是175%∗50%=87.5%。隨著時間推移,大數定律下的內部收益率將是年化-12.5%,將不可避免地破產。
2.3 怎麼回事兒?
你可能會覺得上面的結論很奇怪甚至是錯誤的。
實際上,期望值是一個理論量,用於衡量我們在“同時”複製給定的“賭博”行為會發生什麼情況。但其實,每次“賭博”是依次進行的,結果會隨時間推移而形成。
帶入數字,當我們按照“-50%/+75%”的贏率一遍又一遍地賭博,每次都將資金再投資,期望值就會大幅增長,這主要是因為只有很少幾條路徑都能完全正確,從而帶來天文數字般的回報。但隨著時間的推移,這些路徑在所有可能路徑中所佔的比例越來越小,而我們實際看到其中一條路徑實現的機率也縮小到零。
2.4 再平衡的價值
面對波動的影響,即使期望值可能是正的投資決策,也有必要保留部分資金。這樣,當出現問題時,可以減少損失,從長遠來看會帶來複合收益。
當價格上漲時,平倉部分頭寸以鎖定利潤,以防價格再次下跌。當價格下跌時,有時有必要低價買入獲得預期的未來回報。
在某些情況下,最佳策略是不斷調整投資組合,以使將固定比例的財富投資到每個頭寸上,例如一半現金,一半風險資產。但這並不總是最佳的平衡,一般來說,你希望投資組合中的風險資產越多,其回報率相對於其波動性越高。
重新平衡長期財富增長的好處可能是巨大的,並且可能意味著盈利與破產之間的區別。即使每筆再平衡交易的價格都不利,並造成瞬時損失,結果也是如此。
2.5 煉金術
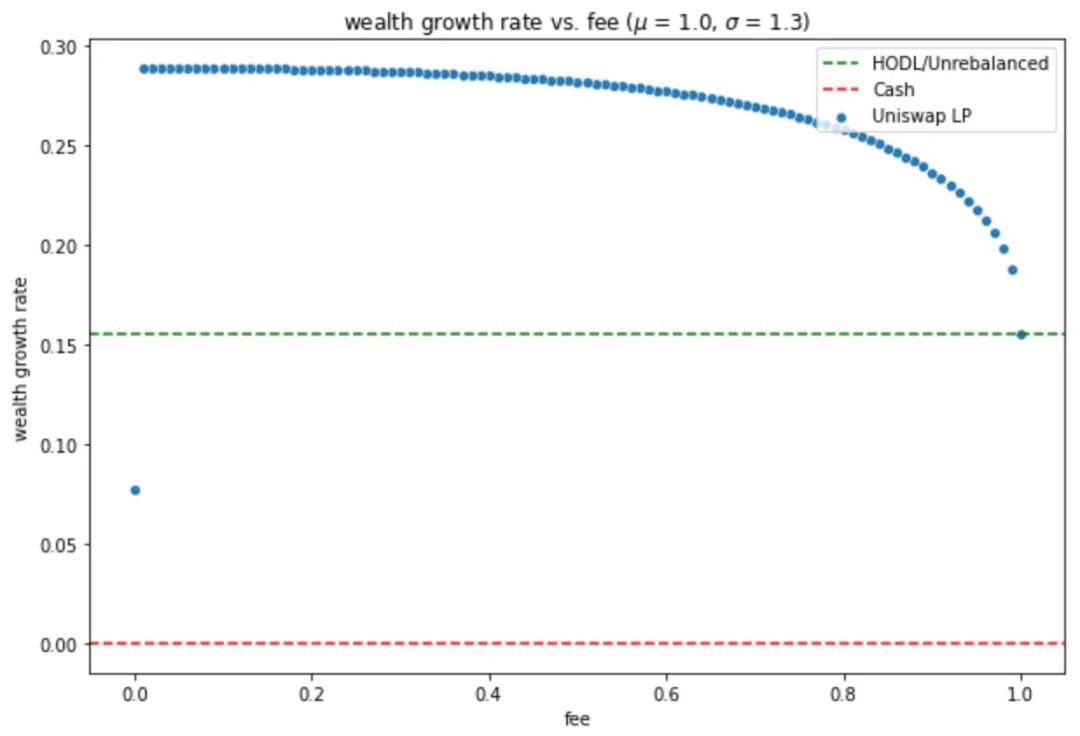
費用從0%起的資產增長率
在上面的設定中,以最小的成本更頻繁的進行再平衡,將對LP有益。因此需要將費用設置為>0%,以降低價格波動率就可以觸發再平衡。但是當費用恰好=0%時,再平衡的所有好處就會消失,並且大概率,LP要比持有非再平衡組合時的收益更差。
Uniswap使用“常數乘積”不變,這意味著在沒有費用的情況下,每筆交易必須保持儲備金餘額的乘積不變。本文表示為Rα Rβ=C ,儘管已經熟悉Uniswap的讀者可能更習慣於x*y=k。
但是,事實證明這個C 必須是數量增加的,才能使再平衡為我們提供財富增長。在免費的情況下, C會保持不變,就沒有財富增長的引擎。
在Uniswap或前文的設置中實施的非0%的費用,可確保C每筆交易都增加。 C隨時間推移增加,意味著儲備金餘額不僅在增長,而且還在保持著平衡,從而提供了收益。
3 數學
綜上所述,現在可以準確地回答Charlie Noyes提出的問題。重複說明一下,他們關注的是Uniswap一類的AMM的財富增長率,這種AMM收取1−γ 百分比的費用,在現金和一種資產之間形成市場,而這種資產的價格以幾何布朗運動的形式變動,帶有參數μ (偏移)和σ (波動率).。
3.1 LP資產的增長率
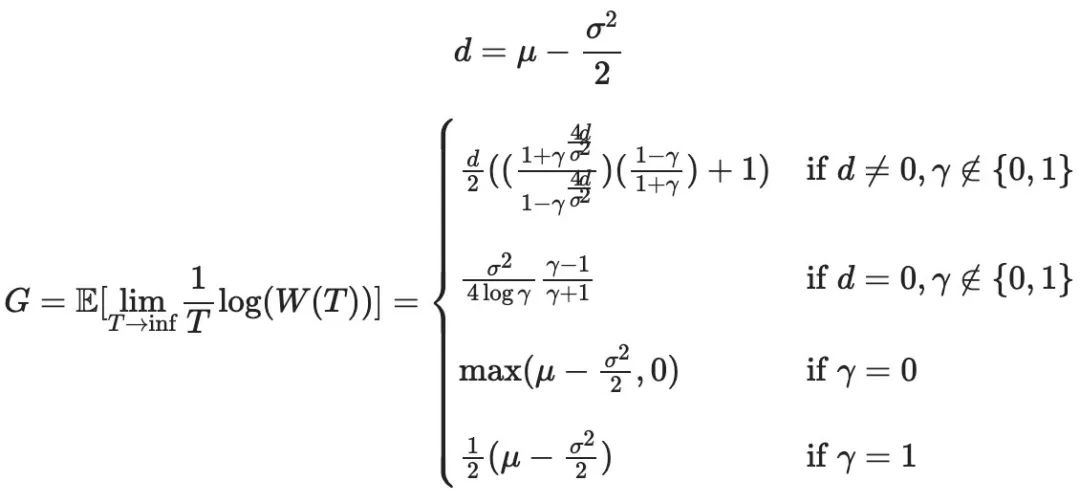
3.2 最優費用與超額收益
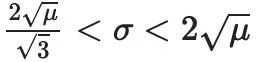
當且僅當μ>0 和時,成為LP比持有一半現金和一半代幣的非再平衡投資組合有更多收益。
在這種情況下,LP應將他們的費用設置為盡可能低的值而不是0%,他們的資產增長率將約為μ/2 - σ²/8。
3.3 解釋
由於“幾何布朗運動”模擬複合增長,因此它們也會受到波動阻力的影響,在數學上可以將GBM的資產增長率表示為-σ²/2:
G=μ-σ²/2
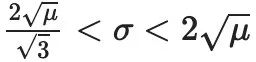
這意味著在範圍內,Uniswap上的LP對應於資產增長率為-μ
這個結果顯示,再平衡能夠抵消部分基礎資產波動性的影響。
另一方面,如果沒有波動性影響的平均收益為正:
如果波動性帶來的損失超過其平均回報的200%,Uniswap的再平衡將不能消除足夠的波動性影響,這種情況最好還是持有現金。如果波動性帶來的損失低於其平均回報的66%,那麼通過Uniswap進行再平衡來抵消波動性影響的代價將是不值得的,此時最好只是持有資產。在此範圍內,成為Uniswap的LP可以創造收益。
